
「数秘術って実は数学と関係があるの?神秘的な占いと科学的な数学がどうつながっているのか知りたい!」
数秘術は古代から伝わる神秘的な占術として知られていますが、その根底には数学的な法則や原理が隠されていることをご存知でしょうか。一見すると相反するように思える神秘と科学の世界ですが、実は深いところでつながっているのです。
- 数秘術の計算方法にはどんな数学的原理があるの?
- 数秘術と数論や幾何学にはどんな関連性があるの?
- 現代数学の視点から見た数秘術の科学的根拠は?
今回はそんな疑問にお答えするため、『数秘術と数学的関係』について詳しくお伝えしていきます!さらに、数秘術の背後にある数学的法則や、科学的視点から見た数秘術の興味深い側面も紹介していきますので、最後までお読みください!
数秘術とは?数学との基本的な関係性
数秘術とは、数字に宿る意味や波動を読み解き、人の運命や性格を占う手法のことです。
この占術は一見すると神秘的で非科学的に思えるかもしれません。しかし、その根底には明確な数学的法則があります。数秘術の最も基本的な操作である「数字の還元」は、実は数学でいう「合同式」や「mod 9の剰余演算」と密接に関連しているのです。
例えば、数秘術では生年月日などの数字を全て足し、一桁になるまで計算します。1985年5月7日生まれなら、1+9+8+5+5+7=35、さらに3+5=8となって「8」が導き出されるわけです。この操作は数学的に見れば「mod 9」の計算と同じ原理なのです。
また、数秘術で用いられる9つの基本数字(1〜9)のシステムは、十進法の特性を利用したものであり、数学的に見れば巧妙な周期性を持っています。このように、数秘術の背後には数学的な構造が隠されているのです。
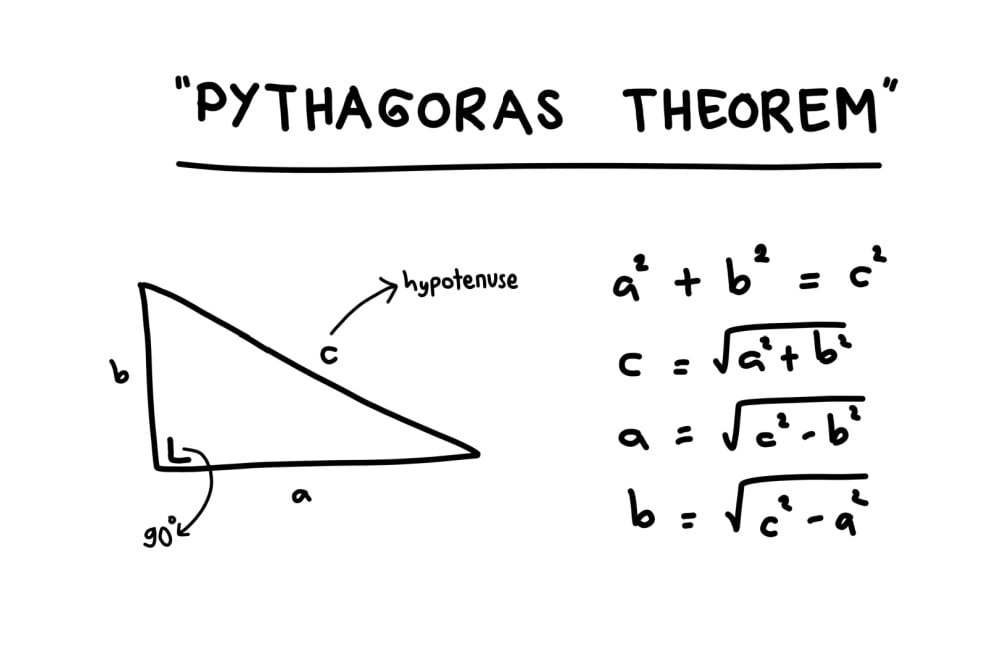
このような関係性は、古代の哲学者や数学者たちが数の神秘に魅了され、数秘術と数学の両方を探求していたことに由来しています。特にピタゴラスは「万物は数である」という思想のもと、数の神秘と数学的法則の両方を追求した人物として知られているのです!
ピタゴラスの貢献 – 数秘術と数学の父

数秘術と数学の関係を語る上で、避けて通れないのが古代ギリシャの哲学者ピタゴラスの存在です。
紀元前6世紀に活躍したピタゴラスは、現代でも中学校で習う「ピタゴラスの定理」で有名な数学者であると同時に、西洋数秘術の基礎を築いた人物でもあります。彼は数を単なる計算の道具としてだけでなく、宇宙の根本原理として捉えていました。
ピタゴラスとその弟子たちは、数の持つ性質を詳細に研究しました。例えば、「完全数」と呼ばれる、自分自身を除く約数の和が自分自身と等しくなる数(例:6=1+2+3)や、「友愛数」と呼ばれる、お互いの約数の和が相手の数になるペアなど、数の持つ不思議な性質を発見したのです。
また、ピタゴラスは音楽と数学の関係も発見しました。弦の長さが2:1の比率になると音程がオクターブになるなど、音楽の調和と数の比率に深い関連があることを示したのです。この発見は、数が物理的な現象を支配しているという彼の信念を強化しました。
実際、ピタゴラス教団では数字には神秘的な意味があると考えられていました。「1」は統一と創造の数、「2」は対立と二元性、「3」は調和と完全性、「4」は安定と物質世界を表すなど、数字に哲学的な意味を見出したのです。
このように、ピタゴラスの研究は純粋な数学と神秘的な数秘術の両方にまたがるものでした。現代の視点から見れば、科学と神秘学が分離していない時代の産物ですが、彼の貢献によって数秘術は数学的な基盤を得ることになったのです!
数論と数秘術 – 素数、完全数、フィボナッチ数列
数秘術と最も関連の深い数学分野の一つが「数論」です。
数論は整数の性質を研究する数学の分野で、素数、約数、合同式などを扱います。特に素数(1と自分自身以外に約数を持たない数)は、数論の中心的なテーマであると同時に、数秘術でも重要な意味を持つとされているのです。
例えば、数秘術では「7」は神秘的で精神性の高い数字とされています。数学的に見ても、7は素数であり、他の数に分解できない「独立した」性質を持っています。このような素数の「還元不可能性」は、数秘術での解釈と数学的に見事に一致している点が興味深いところです。
また、完全数(約数の和が自分自身と等しくなる数)も数秘術と関連があります。最小の完全数である「6」は、数秘術では調和と責任の数とされ、約数である1、2、3の和が6になるという数学的性質と、その象徴的な意味が共鳴しているのです。
さらに、フィボナッチ数列(1, 1, 2, 3, 5, 8, 13…)も数秘術と関わりがあります。この数列は自然界の様々な場所に見られ、黄金比(約1.618)と密接に関連しています。数秘術では、このような自然界の数学的パターンが持つ調和と美を重視し、宇宙の秩序を表す証拠と見なしているのです。
数論のこのような側面は、数秘術が単なる迷信ではなく、数の持つ実際の特性や関係性に基づいている可能性を示唆しています。古代の数秘術師たちは、直感的に数の持つ特別な性質を感じ取り、それを神秘的な言葉で表現していたのかもしれません!
幾何学と数秘術 – 神聖幾何学の法則

数秘術と数学の関係は、幾何学の分野にも広がっています。
特に「神聖幾何学」と呼ばれる分野は、数秘術と深い関わりを持っています。神聖幾何学とは、宇宙の設計図とも言える幾何学的パターンを研究する分野で、古代から神殿や聖堂の設計など、様々な場所で活用されてきました。
例えば、五芒星(ペンタグラム)は数秘術的には「5」に関連し、保護や知恵を象徴するとされています。数学的に見ると、この図形は黄金比に基づく比率を持ち、内部に無限に五芒星を描けるという不思議な性質があるのです。
また、「フラワー・オブ・ライフ」と呼ばれる幾何学的パターンは、重なり合う円が作る複雑な模様で、生命のパターンを表すとされています。この図形からは、プラトンの立体(正四面体、正六面体、正八面体、正十二面体、正二十面体)など、様々な重要な幾何学的形状を導き出すことができるのです。
数秘術では、こうした幾何学的パターンが持つ美しさや調和が、宇宙の根本的な法則を表していると考えられています。実際、これらの図形には数学的に興味深い性質が多く、単なる装飾以上の意味があるのです。
神聖幾何学の原理は、現代の科学でも再発見されています。例えば、結晶構造や生物の成長パターン、さらには素粒子物理学で見られる対称性など、ミクロからマクロまで様々なスケールで同様のパターンが観察されているのです。
このように、数秘術と幾何学には深い関連性があり、古代の叡智が現代の数学や科学の発見と響き合う部分があることは非常に興味深いことといえるでしょう!
モジュラー演算と数秘術の計算法
数秘術の基本的な計算法である「数字の還元」は、数学的には「モジュラー演算」(合同式、剰余演算)と密接な関連があります。
数秘術では、例えば生年月日や名前に対応する数字を全て足し、一桁になるまで足し算を繰り返します。この操作は数学的に見れば「mod 9」の計算とほぼ同じです。mod 9とは、9で割った余りを求める演算のことで、例えば25 mod 9 = 7(25÷9の余りは7)となります。
ただし、数秘術では結果が9になる場合はそのまま9とし、0になる場合は9とするため、厳密には「mod 9」ではなく「数字根」(digital root)と呼ばれる操作に近いのです。数字根は数学でも研究されており、様々な興味深い性質が知られています。
例えば、任意の数の数字根を計算する別の方法として、「その数を9で割った余りを求める(ただし余りが0の場合は9とする)」という計算方法があります。これは、19世紀の数学者フェルマーが発見した性質で、数秘術の計算を大幅に簡略化できるのです。
また、数字根には面白い性質があります。例えば、2つの数の和の数字根は、それぞれの数字根の和の数字根に等しいという性質です。これにより、大きな数字の計算も簡単に行うことができます。
このように、数秘術の計算法は単なる神秘的な手法ではなく、数学的に意味のある操作なのです。古代の数秘術師たちは、このような数学的な性質を直感的に捉え、それを神秘的な体系として発展させたのかもしれません。
モジュラー演算は現代数学でも重要な役割を果たしており、暗号理論やコンピュータサイエンスなど幅広い分野で応用されています。数秘術と現代数学が共有するこの基本的な演算は、両者の意外なつながりを示す好例といえるでしょう!
数秘術の周期性と数学的パターン

数秘術の興味深い特徴の一つが「周期性」です。この周期性は、数学的な視点から見ると非常に興味深いパターンを示しています。
数秘術では、1から9までの数字がそれぞれ固有の意味を持ち、この9つの数字が繰り返し現れるサイクルが存在します。例えば、「ライフパスナンバー」という生年月日から導き出される重要な数字は、必ず1から9のいずれかになります(場合によっては11、22、33などのマスターナンバーもありますが)。
この「9の周期性」は、十進法の特性と密接に関連しています。数学的に見ると、これは「mod 9」の周期性そのものです。1, 10, 19, 28…という数列は全て数字根が1になり、2, 11, 20, 29…は全て数字根が2になるといった具合に、9で規則的なパターンが繰り返されるのです。
また、「数の序列」と呼ばれる興味深いパターンも存在します。例えば、9を掛けた時の積の数字根は常に9になります(9×1=9、9×2=18→1+8=9など)。また、9で割り切れる数の数字根は常に9になるという性質もあります。
さらに、数秘術では「カバラの還元表」と呼ばれる文字と数字の対応表が用いられることがありますが、これもアルファベット26文字を1〜9の数字に対応させるための数学的な変換表と見ることができます。
このような周期性やパターンは、単なる偶然ではなく、数字の本質的な性質に基づいています。実際、数論では「数字根」の性質について多くの研究がなされており、数学者たちも数字の持つこうしたパターンに魅了されてきたのです。
数秘術がこうした数学的パターンを認識し、それに意味を見出してきたことは、決して不思議なことではないのかもしれません。古代の叡智が、直感的に数の持つ法則性を捉えていた可能性を示唆しているのです!
統計学と数秘術 – 偶然と必然の境界
現代数学の視点から数秘術を見る時、統計学の知見も非常に興味深い視点を提供してくれます。
統計学では「ランダム性」と「パターン」の関係を研究します。一見ランダムに見える現象の中にもパターンが存在したり、逆に明確なパターンがあるように見える現象が実は偶然の産物だったりすることがあるのです。
数秘術の観点では、例えば特定の数字が人生で繰り返し現れることに意味を見出します。統計学的に見れば、これは「クラスタリング錯覚」(実際にはランダムな事象が集中して起こっているように感じる認知バイアス)の可能性もあります。
しかし、興味深いことに、カール・ユングのような心理学者は「シンクロニシティ」という概念で、単なる統計的偶然を超えた意味のある偶然の一致があると主張しています。このような視点は、数秘術的な解釈と現代心理学の架け橋となっているのです。
また、「バースディパラドックス」という統計学の有名な問題があります。これは、23人以上の集団では50%以上の確率で同じ誕生日の人が存在するという、直感に反する事実です。このように、数に関する私たちの直感は必ずしも正確ではなく、数学的に厳密に分析すると意外な結果が得られることがあるのです。
数秘術においても、統計的な観点から検証可能な仮説もあります。例えば「特定の数字を持つ人には共通の特徴がある」という主張は、大規模なデータを用いて検証することが理論的には可能です。実際、一部の研究者はこのような試みを行っていますが、科学的に確立された結論には至っていません。
このように、統計学の視点は数秘術と科学の間の興味深い対話の可能性を示しています。偶然と必然、パターンと意味の関係について、両者は異なるアプローチを取りながらも、共通の問いに取り組んでいるとも言えるのではないでしょうか!
黄金比とフィボナッチ数列の神秘性
数秘術と数学の両方で重要な概念として、「黄金比」とそれに密接に関連する「フィボナッチ数列」があります。
黄金比(約1.618)は、「最も美しい比率」とも呼ばれ、古代から芸術や建築に用いられてきました。パルテノン神殿やモナ・リザなど、歴史的な芸術作品にもこの比率が見られるとされています。数学的には、線分を2つに分けた時、全体と大きい部分の比が、大きい部分と小さい部分の比に等しくなる独特の比率です。
一方、フィボナッチ数列(1, 1, 2, 3, 5, 8, 13…)は、連続する2つの数の和が次の数になるという単純なルールで生成される数列です。この数列の隣り合う項の比は、項が大きくなるにつれて黄金比に近づくという驚くべき性質があります。
数秘術では、このような数学的な美と調和を持つ比率や数列が、宇宙の根本的な法則や設計図を表していると考えます。実際、フィボナッチ数列は自然界の多くの場所に見られます。花びらの数、ひまわりの種の螺旋配置、貝殻の形など、自然界には驚くほど多くのフィボナッチ数列のパターンが存在するのです。
興味深いことに、フィボナッチ数列の各項の数字根を計算すると、1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6…という24周期の繰り返しパターンが現れます。この周期性も、数秘術的な解釈と数学的な性質の興味深い接点といえるでしょう。
黄金比やフィボナッチ数列は、芸術的感性と数学的厳密性の両方を兼ね備えた概念です。数秘術がこうした「数学的な美」に特別な意味を見出していることは、決して不思議なことではないのかもしれません。
このように、黄金比とフィボナッチ数列は、数秘術と数学の融合点として、両者の深いつながりを象徴しているといえるでしょう!
現代数学者から見た数秘術 – 科学と神秘の対話
現代の数学者や科学者たちは、数秘術をどのように捉えているのでしょうか。
多くの現代数学者は、数秘術を科学的に検証可能な理論とは見なしていません。科学的方法論に基づく検証や反証が難しいためです。しかし、数秘術が持つ数学的構造や、数字のパターンに対する洞察には一定の興味を示す数学者もいます。
例えば、数学者のマーティン・ガードナーは、数秘術的な数の扱いを「レクリエーショナル数学」(娯楽的数学)の一部として取り上げました。彼は数の持つ興味深い性質や、数字根の計算といった数秘術的な操作が持つ数学的側面に光を当てたのです。
また、一部の認知科学者は、人間が数字にパターンや意味を見出す傾向について研究しています。人間の脳は本来、パターン認識に優れており、時には存在しないパターンさえ「見つけてしまう」ことがあります。これは「アポフェニア」と呼ばれる認知傾向で、数秘術的な解釈の心理的基盤となっている可能性があるのです。
一方で、数学史研究者たちは、数秘術と数学の歴史的な関係に注目しています。特に古代や中世において、数秘術的な思想が数学の発展に与えた影響は無視できないものがあります。例えば、「完全数」の研究や「友愛数」の概念は、当初は数秘術的な関心から生まれたものでした。
興味深いことに、現代物理学の一部の理論、特に「弦理論」では、宇宙の根本構造を説明するために高度な数学と幾何学を用います。こうした理論の美しさや調和性は、時に数秘術的な世界観を彷彿とさせるものがあるのです。
このように、現代の科学者や数学者たちは、数秘術そのものを科学として受け入れることはないものの、数秘術が持つ数学的側面や、人間と数の関係性については、学術的な関心を持って研究を続けています。科学と神秘の間の対話は、今なお続いているのです!
数秘術を数学的視点で活用する方法

数秘術を数学的視点から理解することで、より論理的かつ創造的に活用することができます。
まず、数秘術の計算を行う際には、数学的な理解が役立ちます。例えば、大きな数字の数字根を求める際、9で割った余りを利用する方法は計算を大幅に簡略化できます。また、数字の組み合わせから得られるパターンを認識することで、より深い洞察が得られるでしょう。
さらに、数秘術を確率論的な視点で捉えることも有益です。例えば、ある特定の数字が出る頻度を観察し、それが偶然の範囲内かどうかを考えてみることで、主観的な解釈に客観的な視点を加えることができるのです。
実践的な応用として、数秘術と数学の両方の視点を持つことで、パターン認識能力を高めることができます。日常生活の中で繰り返し現れる数字や、重要な出来事に関連する数字のパターンに注目してみてください。それらが単なる偶然なのか、何か意味があるのかを、批判的思考と直感の両方を使って探求するのです。
また、創造的な思考実験として、自分自身の「数的シグネチャー」(誕生日や名前から導き出される数字のパターン)を探ってみることも興味深いでしょう。それらの数字が持つ数学的特性(素数か否か、完全数との関係など)と、数秘術的な意味の両方を考えることで、新たな気づきが得られるかもしれません。
教育的な観点では、数秘術は数学への興味を引き出すための入り口として活用できます。数の持つ神秘的な側面に興味を持った子どもたちが、その後数論やパターン認識などの本格的な数学へと進む例は少なくありません。
このように、数秘術と数学を対立するものではなく補完し合うものとして捉えることで、両者の知恵を最大限に活かすことができるのです。論理と直感、科学と神秘の境界を行き来することで、より豊かな数の世界を体験してみてはいかがでしょうか!
まとめ:数秘術と数学の調和を見出す
数秘術と数学の関係を探ってきましたが、両者は対立するものではなく、多くの共通点や交点を持つことがお分かりいただけたでしょうか。
数秘術の基本的な計算法であるモジュラー演算(mod 9)は、れっきとした数学的操作です。また、数秘術で重視される周期性や対称性、黄金比といった概念は、数学でも重要な研究対象となっています。古代ではピタゴラスのように、数秘術と数学の両方を探究した賢人もいました。
一方で、両者のアプローチには明確な違いもあります。数学が論理的証明や検証可能性を重視するのに対し、数秘術は直感的理解や象徴的解釈を重視します。数学が「どのように」機能するかに焦点を当てるなら、数秘術は「なぜ」そうなるのか、その意味に焦点を当てるとも言えるでしょう。
現代の視点では、数秘術を科学的理論と見なすことはできませんが、数の持つパターンや特性への洞察、人間と数の関係性についての考察など、数秘術から学べる点も少なくありません。
数秘術と数学の調和を見出すには、どちらか一方だけを絶対視するのではなく、両者の視点を柔軟に取り入れる姿勢が大切です。数学的な厳密さと数秘術的な直感の両方を活かすことで、数の世界をより豊かに理解することができるでしょう。
数秘術に興味がある方は、ぜひその背後にある数学的原理にも目を向けてみてください。また、数学を学ぶ方は、時に数秘術的な視点から数の持つ美しさや神秘性を感じてみることも、新たな発見につながるかもしれません。
論理と直感、科学と神秘の間のバランスを探ることで、数の世界がより多面的に、より深く理解できるようになるのではないでしょうか!





